





| Portada Blogs Álbumes Notas Herramientas Usuarios Ayuda |
| Blog de BLei couRT (cambiar): Página Principal Entradas Historial Estadísticas |
|
Entrada 1 de 3
Siguiendo el esquema de una arquitectura de von Neuman básica (arquitectura en la que se basan la inmensa mayoría de computadoras modernas), nos encontramos con una caja negra singular muy importante, de la que depende en gran medida la velocidad y capacidad de ejecución de la computadora: la unidad aritmético lógica (ALU por su siglas en inglés).
Como su propio nombre indica, la ALU realiza las operaciones aritméticas (tales como sumas, restas, y cosas más o menos complicadas dependiendo del computador) y lógicas (comparaciones, desplazamientos, ANDs, ORs, etc). Los procesadores actuales tienen ALUs muy complejas que hacen muchos tipos de operaciones matemáticas diferentes; el hecho de que una ALU sea capaz de hacer una operación evita tener que emularla por software con la consecuente pérdida de velocidad y potencia. Sin embargo, ALUs complejas incrementan de forma apreciable el número de transistores y componentes necesarios, así como la energía necesaria para su funcionamiento y por ende la cantidad de calor disipado. Son una de las partes más importantes de la CPU, encontrándose al menos una por cada núcleo en los procesadores actuales. Las ALUs usualmente operan sólo con números enteros (en diferentes representaciones), las unidades homólogas que se usan para coma flotante se denominan FPUs (anecdóticamente, hasta los primeros pentiums las FPUs no estaban integradas en el procesador y eran opcionales, era lo que se llamaba co-procesador). Archivado en: Hardware, Spanish. Entrada 2 de 3
El circuito aritmético más básico de una ALU consiste en un sumador/restador de números enteros. En realidad el circuito es un sólo sumador que convierte uno de los operandos a complemento a 2 cuando debe hacerse una resta (el equivalente a cambiar el signo en notación decimal).
Partimos del diseño básico de un sumador de 1 bit usando dos puertas lógicas (AND y XOR). El resultado de la suma del bit de cada operando se expresa en 2 bits.
Este es el diseño correspondiente a un semisumador (HA, del inglés Half Adder). Para convertirlo en un sumador completo debemos añadir una entrada para el acarreo de la etapa anterior, de forma que podamos usar la composición para crear sumadores completos de N bits.
Este diseño corresponde a un sumador completo (FA del inglés Full Adder) construido con dos HA (resaltados en cuadros amarillos). Como puede verse hay 3 niveles de puertas, y aunque el resultado de la suma 'S' podemos recogerlo tras dos ciclos de reloj, el acarreo resultante para la siguiente fase o para detección de overflow tardará tres ciclos. Es decir, si nuestro procesador funciona a 1Ghz (1 billón de ciclos segundo), podremos hacer (10^9)/3= 333 millones de sumas de 1 bit por segundo (obviando el tiempo de lectura de los operandos desde la memoria principal, el retardo de la lógica de control, del bus de datos, etc). Con FAs podemos construir sumadores de N bits en cascada. Veamos un ejemplo de un sumador de 2 números de 4 bits. 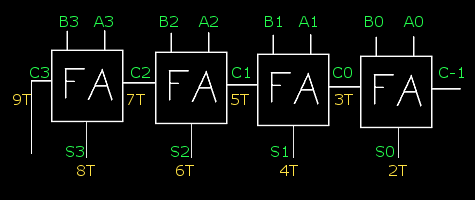 Sumador de 4 bits formado con 4 FAs En verde están marcadas las entradas y salidas de los sumadores completos de un bit (FA), cada sumador tiene que esperar a que el anterior calcula el acarreo entrante, por lo tanto hay un retraso que se va acumulando al no poder actuar todos a la vez en paralelo. Los tiempos para cada salida están marcados en amarillos (la T significa "unidades de tiempo", sean cuales sean). De forma que, para sumar 2 números de 4 bits, tendremos que esperar 9 ciclos o unidades de tiempo hasta tener el último dígito de la suma (C3,S3,S2,S1,S0 respectivamente). En general, si hacemos un montaje de este tipo para sumar 2 enteros de N bits, tardaremos 2N+1 ciclos en completar la operación. Siguiendo el ejemplo anterior, a 1GHz y con este esquema, sólo podríamos hacer (10^9)/9 = 111 millones de sumas de 4bits por segundo. Añadir a este sumador la opción de realizar una resta o una suma a elección, es algo prácticamente trivial que se resuelve pasando uno de los operandos a complemento a 2. Otro añadido interesante es la detección de overflow que activaría el registro correspondiente dentro de la ALU. 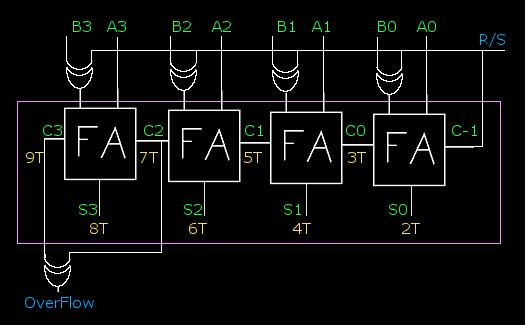 Sumador/Restador de 4 bits con detección de OverFlow NOTA: Los tiempos de la imagen anterior se refieren a los tiempos del circuito sumador, habría que añadir un ciclo para la presunta conversión a complemento a 2 y otro ciclo más para detectar el desbordamiento. Archivado en: Hardware, Spanish. Entrada 3 de 3
Es posible adelantar el resultado usando un circuito anticipador de acarreo (CLA, del inglés "Carry look-ahead adder").
Si nos fijamos, la generación de un acarreo en la etapa i viene dada por: Gi=ai*bi Y su propagación por: Pi: ai+bi De forma que podemos saber si en la etapa i habrá acarreo usando: Ci=Gi+Pi*C(i-1) Si desglosamos para cada etapa el acarreo necesario y simplificamos la ecuación, podemos adelantarnos usando sólo las sumas de cada etapa y el primer acarreo (está muy bien explicado en la wikipedia), de forma que para el caso del sumador de 4bits, podemos tener el resultado en 4 ciclos frente a los 9 necesarios sin el anticipador de acarreo. 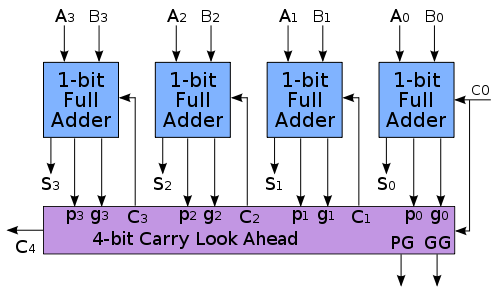 C1, C2 y C3, proporcionados por el CLA, tomarían su valor correcto en 3T, S0 en 2T, y S1, S2, y S3 en 4T. Conseguimos de esta forma un aumento de velocidad del 125% (más del doble), lo cual no está nada nada mal. Archivado en: Hardware, Spanish.
|
Páginas
Puntuación
WARNING!!! About... Estadísticas
6003 Días
4478 Visitas
6 Posts
Postea una de
cada 746 visitas Licencia
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||